6 A Monopoly simulation

Now you will use to simulate simplified games of Monopoly (https://en.wikipedia.org/wiki/Monopoly_(game)). In addition, there are also many tutorials and guides on the Web describing how to produce computer simulations for Monopoly. You are welcome to read and use these examples to inspire your work.

6.1 Moving around the board

A Monopoly board has 40 spaces. Players take it in turns to roll two dice and traverse around the board according to the sum of the dice values.

Use the following code example to simulate turns of a single player:

num_turns <- 100000 # number of turns to take

current_board_position <- 0 # start on the GO space

move_size <- rep(0, num_turns)
positions_visited <- rep(0, num_turns)

# use a for loop to simulate a number of turns
for (turn in 1:num_turns) {

  # roll two dice
  die_values <- sample(c(1:6), 2, replace = TRUE)

  # move player position

  # number of positions to move
  plus_move <- sum(die_values)

  # compute new board position
  new_board_position <- current_board_position + plus_move

  # update board position (this corrects for the fact the board is circular)
  current_board_position <- (new_board_position %% 40)

  # store position visited
  positions_visited[turn] <- current_board_position

}

By increasing the number of turns taken, what distribution does the set of simulated board positions converge towards? Show this graphically using the histogram function.

hist(positions_visited, breaks = seq(0, 40, len = 41), right = FALSE)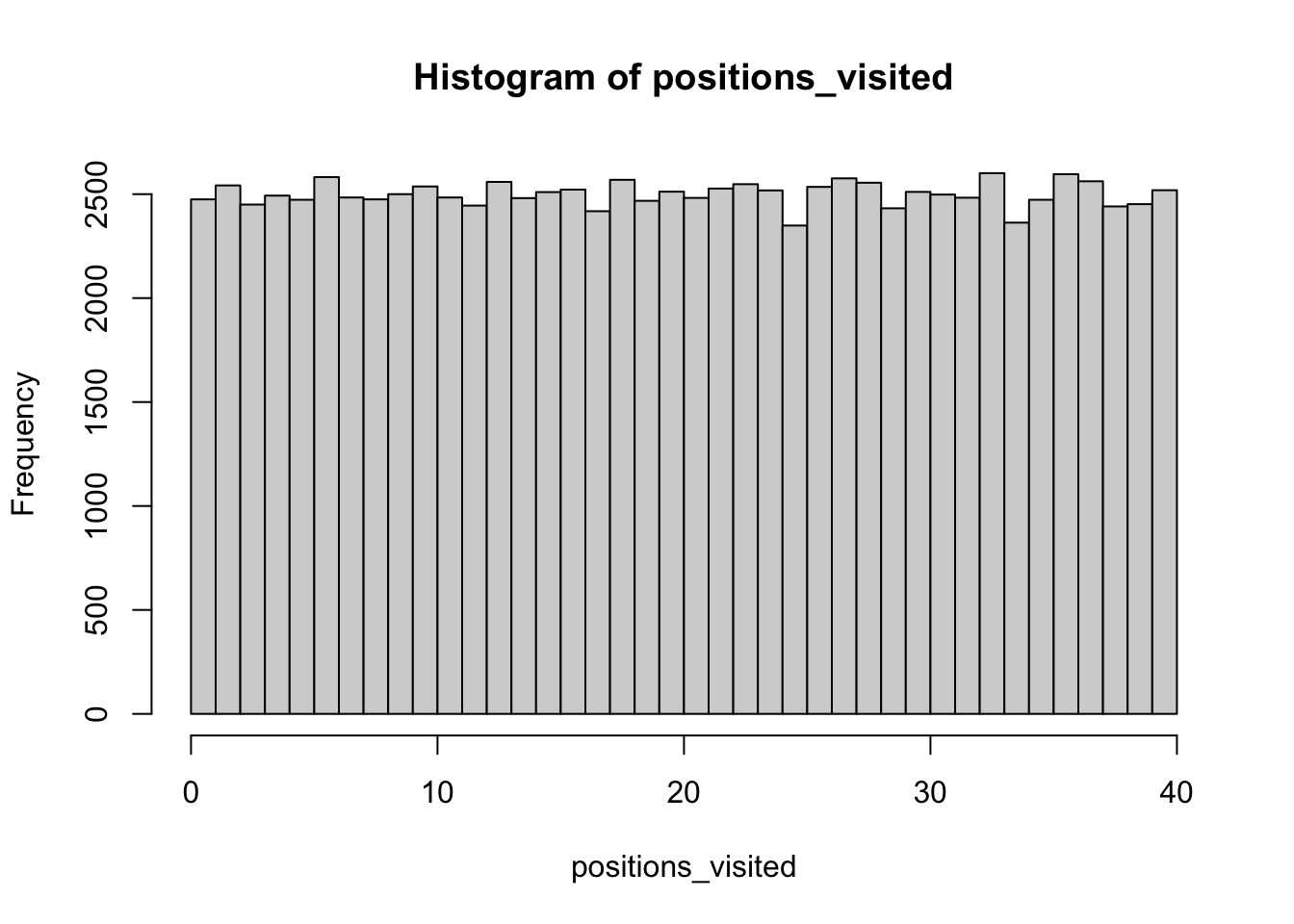

6.2 Going to Jail

If a player lands on to Go To Jail space they must move immediately to the Jail space. Extend your code to include the possibility of going to jail. Here, assume that once in jail, the player continues as normal on the next turn.

 num_turns <- 100000 # number of turns to take

current_board_position <- 0 # start on the GO space
go_to_jail_position <- 30 # the go to jail space
jail_position <- 10 # jail space

move_size <- rep(0, num_turns)
positions_visited <- rep(0, num_turns)

# use a for loop to simulate a number of turns
for (turn in 1:num_turns) {

  # roll two dice
  die_values <- sample(c(1:6), 2, replace = TRUE)

  # move player position

  # number of positions to move
  plus_move <- sum(die_values)

  # compute new board position
  new_board_position <- current_board_position + plus_move

  # if land on GO TO JAIL square, then go backwards to the JAIL square
  if (new_board_position == go_to_jail_position) {
    new_board_position <- jail_position
  }

  # update board position (this corrects for the fact the board is circular)
  current_board_position <- (new_board_position %% 40)

  # store position visited
  positions_visited[turn] <- current_board_position

}

What is the distribution of board positions during a long game?

hist(positions_visited, breaks = seq(0, 40, len = 41), right = FALSE)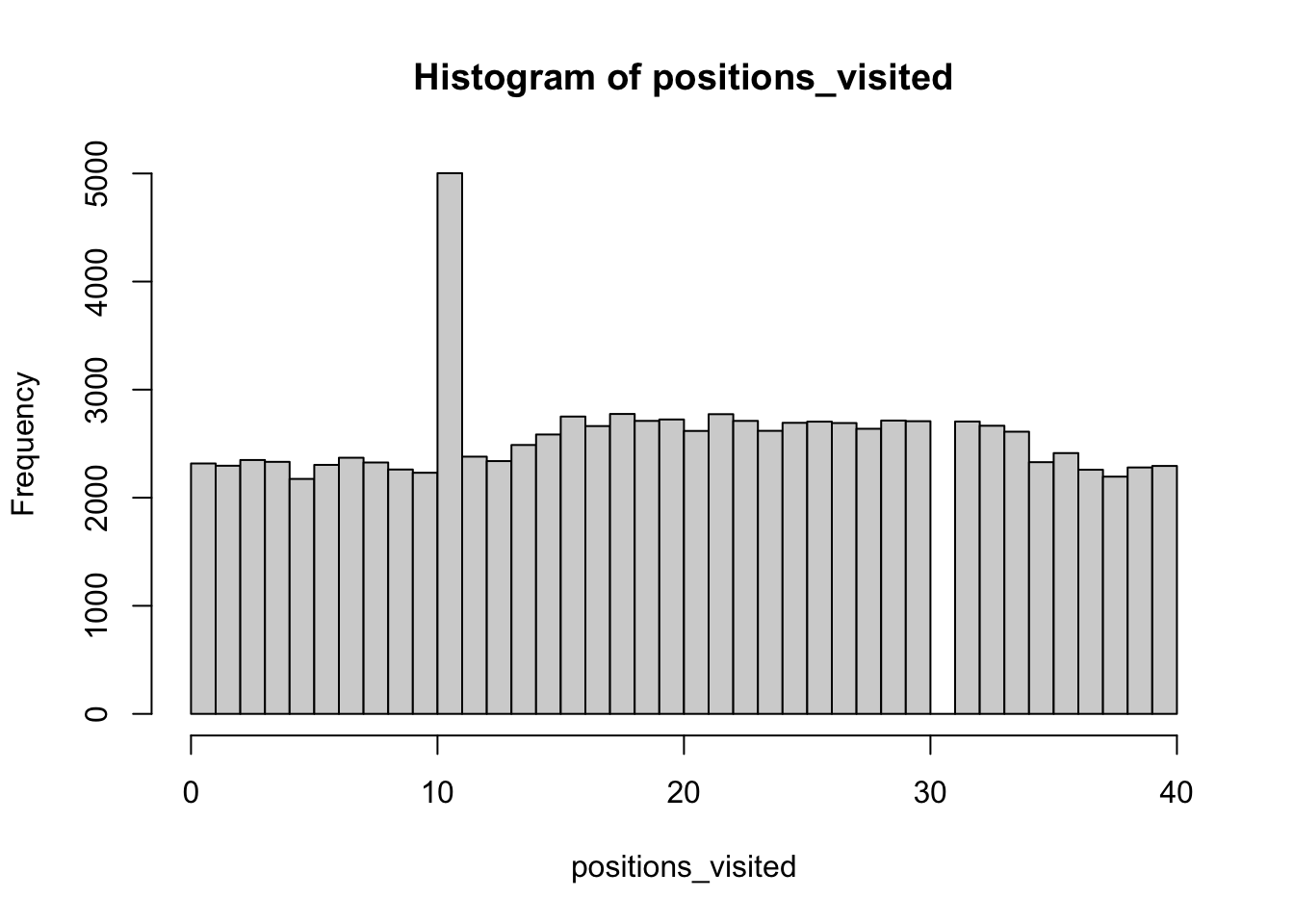

Can you explain this result qualitatively?

You can also go to jail, if you roll three doubles (both dice having the same value) in a row. Update your code to allow for the possibility of going to Jail with three doubles. How does the distribution of board positions change?

num_turns <- 100000 # number of turns to take

current_board_position <- 0 # start on the GO space
go_to_jail_position  <- 30 # the go to jail space
jail_position <- 10 # jail space

move_size <- rep(0, num_turns)
positions_visited <- rep(0, num_turns)

# use a for loop to simulate a number of turns
for (turn in 1:num_turns) {

  # set double counter to zero
  double_counter <- 0

  # roll (max) three times
  for (j in 1:3){

    # roll two dice
    die_values <- sample(c(1:6), 2, replace = TRUE)

    # if we have rolled a double for the third time, we proceed straight to jail
    if ((die_values[1] == die_values[2]) & (double_counter == 2 )) {
      current_board_position <- jail_position
      break
    }

    # otherwise

    # move player position

    # number of positions to move
    plus_move <- sum(die_values)

    # compute new board position
    new_board_position <- current_board_position + plus_move

    # if land on GO TO JAIL square, then go backwards to the JAIL square
    if (new_board_position == go_to_jail_position) {
      new_board_position <- jail_position
    }

    # update board position (this corrects for the fact the board is circular)
    current_board_position <- (new_board_position %% 40)

    # break out of loop if we roll a non-double
    if (die_values[1] != die_values[2]) {
      break
    } else { # increment double counter
      double_counter <- double_counter + 1
    }

  }

  # store final position visited
  positions_visited[turn] <- current_board_position


}


hist(positions_visited, breaks = seq(0, 40, len = 41), right = FALSE)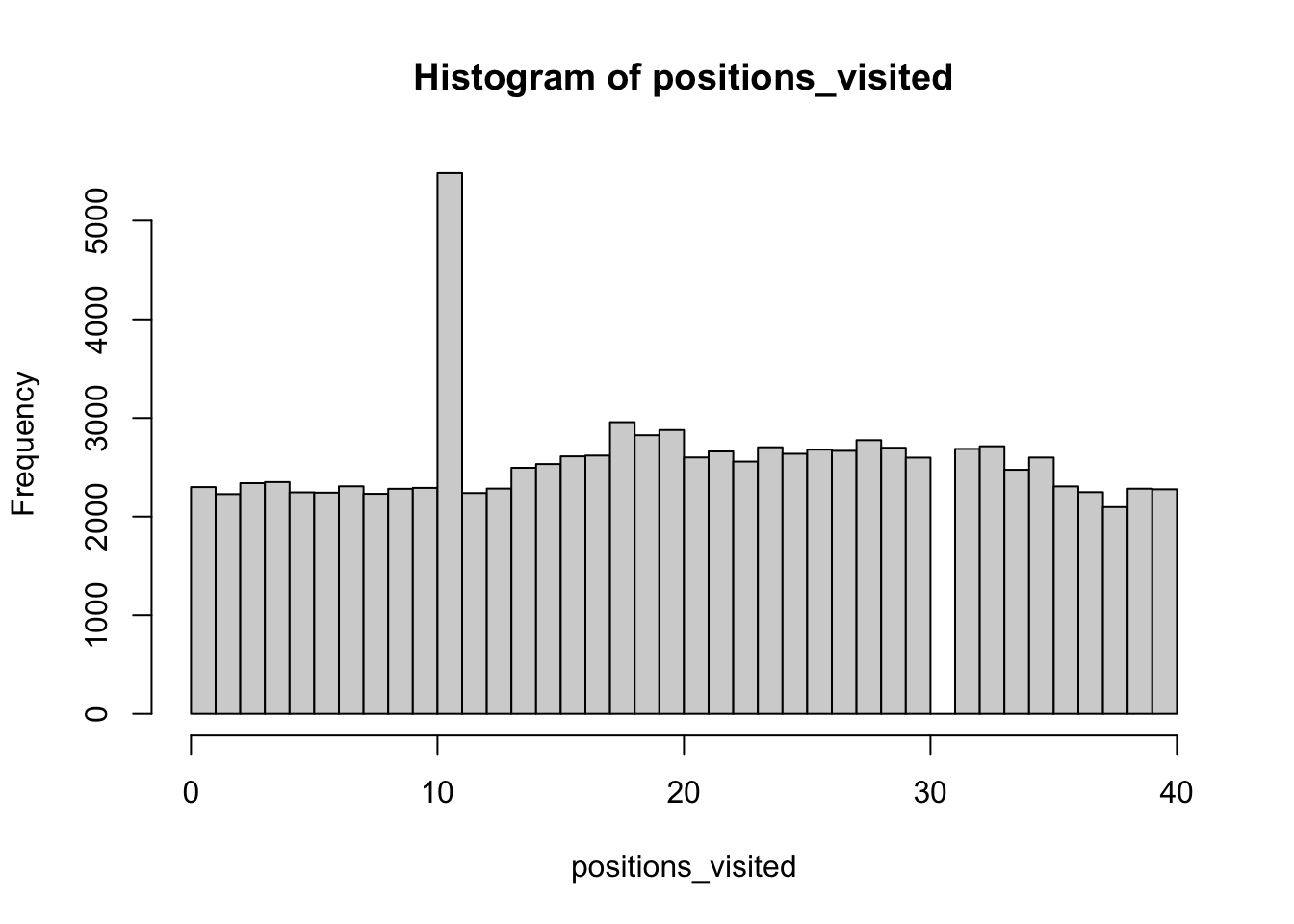

Adding the rolling doubles feature doesn’t seem to change much. We might expect this since rolling three doubles is a very unlikely event!

6.3 Further Exercises

Now consider building a more complex Monopoly simulation by incorporating more complex aspects of the game such as:

the purchase of properties
a ledger for each player
chance and community cards

You will need to think carefully about the simplifying assumptions you will make to make the task achievable. Do not be over-ambitious. For example, you might initially assume that players will not build houses/hotels on properties.

Here are some questions to answer with your simulations:

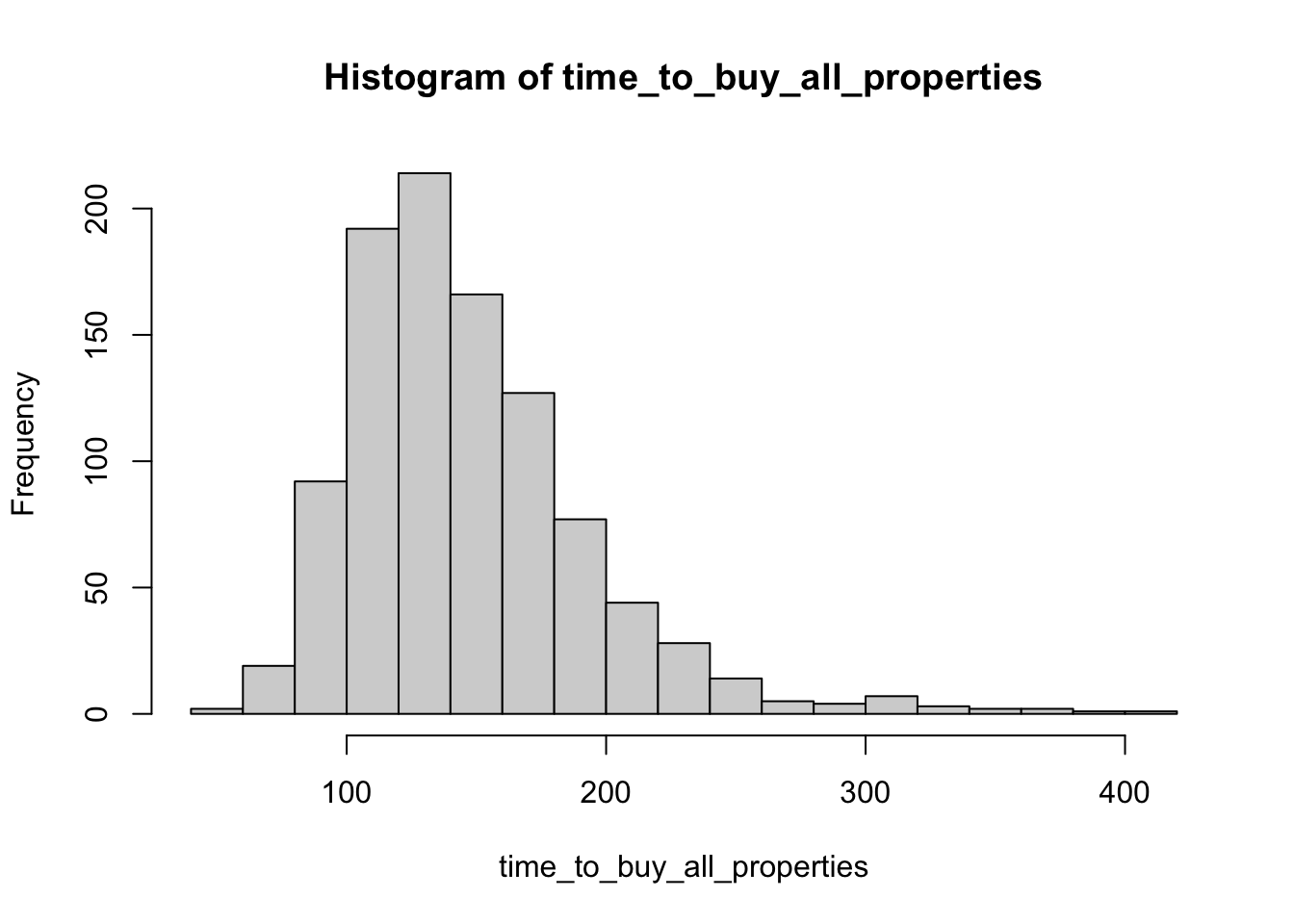
How many turns does it take before all properties are purchased?
What are the best properties to buy?
How long does it take for a winner to be determined?

For example, the following simple extension of the previous example adds some features to record properties being purchased. This simulation is constructed based on the assumption that a players always buys any free property that land on.

num_games <- 1000 # number of games to play
num_turns <- 1000 # number of turns to take

current_board_position <- 0 # start on the GO space
go_to_jail_position <- 30 # the go to jail space
jail_position <- 10 # jail space
# vector of squares containing properties
properties_that_can_be_bought <- c(1, 3, 5, 6, 8, 9, 11, 12, 13, 14, 15, 16,
   18, 19, 21, 23, 24, 25, 26, 27, 28, 29, 31, 32, 34, 35, 37, 39)


# vector to store number of turns to buy all properties
time_to_buy_all_properties <- rep(0, num_games)

# simulate multiple games
for (game in 1:num_games) {

  positions_visited <- rep(0, num_turns)
  positions_purchased <- rep(0, 40)
  properties_bought <- rep(0, num_turns)

  # use a for loop to simulate a number of turns
  for (turn in 1:num_turns) {

    # roll two dice
    die_values <- sample(c(1:6), 2, replace = TRUE)

    # move player position

    # number of positions to move
    plus_move <- sum(die_values)

    # compute new board position
    new_board_position <- current_board_position + plus_move

    # if land on GO TO JAIL square, then go backwards to the JAIL square
    if (new_board_position == go_to_jail_position) {
      new_board_position <- jail_position
    }

    # update board position (this corrects for the fact the board is circular)
    current_board_position <- (new_board_position %% 40)

    # if we can on a square that can be purchased and which has not been
    # purchased (note R uses 1-indexing for arrays)
    if (positions_purchased[current_board_position+1] == 0) {
      if (current_board_position %in% properties_that_can_be_bought) {
        positions_purchased[current_board_position + 1] <- 1
      }
    }

    # store position visited
    positions_visited[turn] <- current_board_position

    # store number of properties bought
    properties_bought[turn] <- sum(positions_purchased)

    # check if all properties are gone
    if (properties_bought[turn] == length(properties_that_can_be_bought)) {
      time_to_buy_all_properties[game] <- turn
      break
    }


  }

}

hist(time_to_buy_all_properties, breaks = 20)